آموزش مجموعه ها-ریاضی نهم

 

آموزش مجموعه ها-ریاضی نهم

 

مجموعه، بدلیل آنکه یکی از مفاهیمِ غیر قابل تعریف است، تا مدت ها مورد بی توجهی قرار گرفت و ضرورتی بـرای
پرداختن به آن احساس نشد، تا اینکه جورج کانتور، ریاضیدان آلمانی، با مطالعه بر روی مجموعه ها و قوانین حاکم
بر آنها، توجه همگان را به آن جلب کرد.
اهمیت مطالعه بر روی مجموعه ها در این است که اگر ویژگیای برای آنها پیدا کردیم، آنگاه می توانیم نتیجه بگیریم
که آن ویژگی برای تمام پدیده هایی در طبیعت که به صورت مجموعه هستند نیز، وجود دارد.

نکات مهم

Z = {…,−۲,−۱,۰,۱,۲,…} :اعداد صحیح

I = {0,1,2,3,…} :اعداد حسابی

N = {1,2,3,4,…} :اعداد طبیعی

نماد عضویت:∋                                                                نماد عدم عضویت: ∋
نماد زیرمجموعه بودن: ⊃                                                   نماد زیرمجموعه نبودن: ⊃
نماد مجموعه تهی: φ یا {}

نماد مجموعه مرجع: M یا U

۱-علامت “…” در یک مجموعه، به این معناست که اعضای مجموعه با همان روند اعضا ی نوشته شده و همان نظم
و الگو، ادامه می یابند.

٢ -اگر تمام اعضای مجموعه A ، در مجموعه B وجود داشته باشد، آنگاه A” زیرمجموعه”B است.

٣ -اگر دو مجموعه، زیرمجموعه یکدیگر باشند، آنگاه با یکدیگر مساوی خواهند بود.

۴ -هر مجموعه ای، زیرمجموعه خودش است.

۵ -مجموعه تهی، زیرمجموعه تمام مجموعه ها است.

۶” -زیرمجموعه محض” برای مجموعهA ، مجموعه ای است که حداقل یک عضو، کمتر از مجموعه A داشته باشد.

٧ -هیچ مجموعه ای، زیرمجموعه محضِ خودش نیست.

٨ -مجموعه، نمی تواند عضو تکراری داشته باشد. در واقع از بین اعضای تکراری، فقط یکی از آنها باقی می ماند و
بقیه حذف می شوند.

٩ -ترتیب در نوشتن اعضای مجموعه، تأثیر ندارد. یعنی، میتوان ترتیب اعضای مجموعه را به دلخواه جابجا کرد.

١٠ -مجموعه ای که تمام مجموعه ها، اعضای خود را از آن انتخاب م ی کنند “مجموعه مرجع” نام دارد و معمـولاً آن
را با M یا U نشان می دهند.

١١ -تمام مجموعه ها، زیرمجموعه، مجموعه مرجع هستند.

١٢” -متمم مجموعه A ،” مجموعه ای است که اعضای آن در A نباشند. یعنی باید اعضـایی از مجموعـه مرجـع را
انتخاب کنیم، که برای ساختن مجموعه A استفاده نشده اند. متمم مجموعه A را با ‘A نشان می دهند.

١٣-تعداد اعضای یک مجموعه را “عدد اصلی” آن می گویند. عدد اصلی مجموعه A را با (A(n نشان می دهند.

١۴ -اگر همه زیرمجموعه هایA را درون یک مجموعه بزرگ بریزیم، آن را “مجموعـه تـوانی A ” مـی نامنـد و بـا
(A(P نشان می دهند. در واقع (A(P مجموعه ای است که از تمام زیرمجموعه های A تشکیل شده است.

١۵” -اجتماع A و B ، ” مجموعه ای است که همه اعضای مجموعه های A و B را در آن ریخته ایم. آن را به صورت
B ∪ A نشان می دهند.

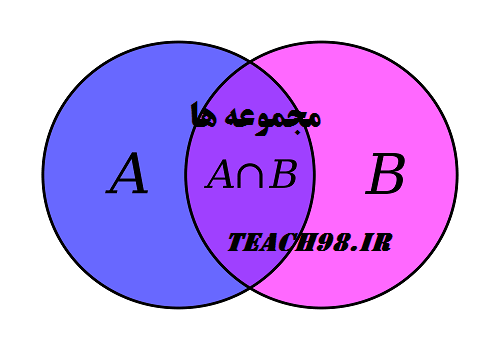
١۶” -اشتراک A و B ،” مجموعه ای است که اعضای مشترک در مجموعه هایA وB را در آن ریخته ایم. آن را به
صورت B ∩ A نشان می دهند.

۲ . n ١٧ -تعداد زیرمجموعه های یک مجموعه n عضوی برابرست با

. n ١٨-تعداد زیرمجموعه های محضِ مجموعه n عضوی برابرست با ۱ − ۲

١٩ -اگر تعداد اعضای یک مجموعه، محدود باشـد، آن را “مجموعـه متنـاهی” گوینـد و در غیـر اینصـورت آن را
“مجموعه نامتناهی” گویند.

٢٠” -نمودار وِن” ، نمایش مجموعه ها با کمک اشکال هندسی است و معمولاً از مستطیل برای نشان دادن مجموعـه
مرجع و از دایره ها برای نشان دادن مجموعه های دیگر استفاده می کنند.

نمونه سوالات

اگر A و B مجموعه های دلخواهی باشند، درستی یا نادرستی هر عبارت را مشخص کنید.

الف)(A∩ B) ⊂ A
ب)(A∪ B) ⊂ (A∩ B)
ج)(A ∩ B) ⊂ (A ∪ B)
د (A ⊂ (A∩ B)